Vier Basisarchitekturen für Klassifikationsmodelle
Autor: H. R. Straub
Deutsche Vorversion (1998) des Kapitels "Four Different
Types of Classification Models" in R. Grütter (Hrsg.): "Knowledge
Media in Health Care: Opportunities and Challenges." Idea Publishing
Group, Herskey / London. Das Buch erscheint ca. Okt. 2001.
Einleitung:
Die Rolle von Klassifikationsmodellen
1: Eindimensionales, hierarchisches Modell
2: Mehrdimensionales, unifokales Modell
3:
Mehrdimensionales, multifokales, unipunktuelles Modell
4: Multifokales, multipunktuelles Modell
Die Rolle von Klassifikationsmodellen
(Reprise)
Zusammenfassung
Jede Klassifikation
vernachlässigt gewisse Aspekte der Realität und hebt andere hervor.
Wenn so detailreich und umfassend und gleichzeitig so klar und einfach
wie möglich klassiert werden soll, spielen neben den inhaltlichen
Aspekten der Klassifikation auch die formalen ihrer Architektur eine
Rolle. Die vorliegende Arbeit stellt vier grundlegend unterschiedliche
Klassifikationsarchitekturen dar und grenzt sie voneinander ab.
Ausgehend vom hierarchischen, linearen Modell werden die Eigenschaften
der Multiaxialität, der Multifokalität und der Multipunktualität
vorgestellt und erklärt. Komplexe Klassifikationen optimieren
Detailreichtum und Modellierungsmöglichkeiten, doch werden vielerorts
einfachere Modelle bevorzugt. Komplexe und simple Klassifikationen
können nebeneinander koexistieren, jede an ihrem Platz. Von einer
realitätsnahen und deshalb komplexen Klassifikation können einfachere
abgeleitet werden, nicht aber umgekehrt.
Stichworte
ICD-10, Begriffsrepräsentation,
Klassifikationssysteme, semantischer Raum, Conceptual Graphs, OOP,
automatische Kodierung.
Summary
Any
classification neglects certain aspects of reality and emphasizes
others. If a classification is meant to be as detailed and
comprehensive and yet at the same time as clear and concise as
possible, it is not only its content that matters but also the formal
aspect of its architecture. This paper describes the fundamentally
different architectures of classification and distinguishes them from
each other. Starting out from the hierarchical linear model, it
expounds the qualities of multiaxiality, multi-focality and
multi-punctuality. Although complex classifications optimize richness
of detail and the potential for modulation, simpler models are often
favoured instead. Complex and simple classifications can coexist
alongside each other, each in its own right. Simple classifications
may be deduced from realistic and therefore complex classifications
and not the other way round.
Keywords
ICD-10, knowledge representation, nomenclature, classification, semantic space, conceptual graphs, OOP, automatic encoding.
Einleitung: Die Rolle von
Klassifikationsmodellen

EDV heisst elektronische
Datenverarbeitung. Daten tragen Informationen - aber welche? Das
Problem wird immer dann offensichtlich, wenn es sehr viele Daten sind.
Dann müssen die Daten nämlich strukturiert werden, um aus ihnen eine
Aussage (=Information) zu gewinnen.
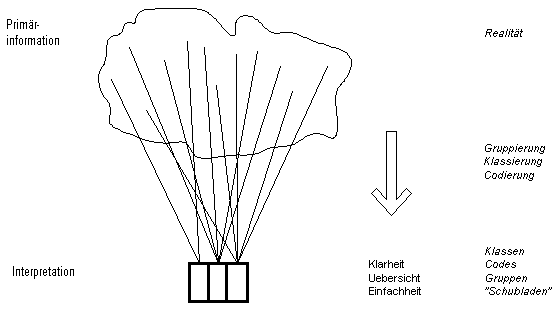
Dabei ist evident:
Die direkt bei den konkreten
Ereignissen erhebbaren Primärinformationen sind reichhaltiger als jede
spätere Interpretation. Die Primärdaten tragen mehr Information in
sich, als je eine Auswertung oder Interpretation benötigt oder
verwenden kann.
Der Prozess der Interpretation
beinhaltet deshalb eine Verarmung, nämlich eine Reduktion der Anzahl
der Daten (=bits). Nur durch die Strukturierung der Daten kann eine
Aussage gemacht werden und dies bedeutet eine Verminderung der
ursprünglichen Gesamtinformation.
Welche Information wird
weggelassen? Die Frage ist keinesfalls banal, denn die Auswahl
entscheidet, welche Information schliesslich übrig bleibt. Man könnte
nun annehmen, dass es immer eine quasi naturgegebene Auswahl gibt.
Dies ist nicht der Fall. Denn die Auswahl liegt nicht nur in den
betrachteten Daten - dem "Objekt" - begründet, sondern auch in der
Absicht der Untersuchung, d.h. im Kontext der Fragestellung - im
"Subjekt" also. Je nach Fragestellung ändert die Sichtweise und somit
auch die Auswahl der für sie relevanten Information.
Um bei diesem
Weglassen bei grösstmöglicher Uebersichtlichkeit trotzdem möglichst
viele Details und Sichtweisen auf der Interpretationsseite zu
bewahren, also um das Produkt
von Uebersichtlichkeit mal Detailreichtum zu optimieren, kommt
der Strukturierung der Information auf der Interpretationsseite und
somit dem Modell der Wissensrepräsentation eine entscheidende
Bedeutung zu. Der vorliegende Text hat diese innere Architektur von
Wissensrepräsentation in Klassifikationen zum Thema und zeigt davon
vier wohlunterschiedbare Modelle, die - eines logisch aus dem anderen
herauswachsend - eine zunehmend realitätsnähere Modellierung der
Begriffsarchitektur erlauben.
1: Eindimensionales, hierarchisches[1] Modell

Die Begriffe
können als "Schubladen" angesehen werden, in welche ähnliche
Gegenstände oder Ereignisse der Realität abgelegt werden. Die Worte
für die Begriffe sind in diesem Bild die Namen, mit denen die
Schubladen angeschrieben sind. Natürlich kann dieser Name auch eine
Zahl oder eine Code-Nummer sein. Codes haben den Vorteil des
geringeren Speicherbedarfs (bei den ersten Computern wichtiger als
heute) und den der Verschleierung (Militär) [2] .

Bei der eindimensionalen Architektur werden die Begriffe einer nach dem anderen aneinander gereiht. Durch die Reihung der Begriffe entsteht bereits eine gewisse Ordnung. Insbesondere können benachbarte Schubladen zusammengefasst werden. Sie bilden dann auf einem höheren Level übergeordnete Einheiten, d.h. die Begriffe sammeln sich zu Oberbegriffen. Der Vorgang kann sich wiederholen und die Oberbegriffe können ihrerseits zu Ober-Oberbegriffen zusammengefasst werden. Aus einer linearen Folge entsteht so ein hierarchischer Baum:
|
|
Der Oberbegriff
ist dabei implizit, d.h. durch das System gegeben. Er muss im
konkreten Einzelfall nicht mehr mitgenannt werden, sondern versteht
sich von selbst. So impliziert im ICD-10-Code die Angabe A00.1
(El-Tor-Cholera):
- den
Oberbegriff A00 (Cholera)
- den
Ober-Oberbegriff A00-A09 (infektiöse Darmkrankheit)
- den
Ober-Ober-Oberbegriff A00-B99 (Bestimmte infektiöse oder parasitäre
Krankheit)
Diese
Implikationen müssen im konkreten Fall nicht mehr genannt werden. Sie
sind durch den einfachen Begriff (El-Tor-Cholera) bereits automatisch
durch das System mitgenannt (und auch in keinem Fall mehr
wegbedingbar). Die Oberbegriffe enthalten bezogen auf die
Unterbegriffen keine zusätzliche Information.
Das
hierarchische System setzt somit ein Regelwerk voraus, das über die
einfache Nennung der Endbegriffe hinausgeht. Im konkreten Einzelfall
aber - zB. zur Datenübermittlung oder Datenspeicherung - genügt die
Angabe des tiefsten Unterbegriffes, d.h. des endständigen Blattes,
welches alle übergeordneten Begriffe systemimmanent immer mitträgt.
Der auf den ersten Blick zweidimensional erscheinende Hierarchiebaum
kann somit mit Leichtigkeit auf eine eindimensionale Reihung
abgebildet werden. Diese problemlose Abbildbarkeit auf ein lineares
Modell macht das hierarchische Modell so einfach im Handling in
Computersystemen.
Der ICD-10-Code
ist ein schönes Beispiel für die enge Verwandtschaft des unilinearen
Codes mit der hierarchischen Klassifikation. Die meisten anderen Codes
im Gesundheitswesen folgen ebenfalls dem hierachischen,
eindimensionalen Typ.
2:
mehrdimensionales, unifokales Modell
Beim eben beschriebenen,
eindimensionalen Modell kann die gezeichnete Achse als Dimension eines
Raumes angesehen werden. Der Raum ist bei der ICD-10 der linear
geordnete Raum der "Zahlen" A00.0 bis Z99.9 [3] . Jeder Begriff entspricht
einem Ort in diesem Raum, auf dieser Achse, in dieser Dimension.
Wenn das System
eindeutig sein soll, dann kann für einen Begriff nur ein Wert
repräsentativ sein, bzw für einen Oberbegriff ein Bereich benachbarter
Werte. Ein Begriff darf keine Repräsentation haben, bei der zwei oder
mehr voneinander getrennte Werte gleichzeitig genannt werden müssen.
Verschiedene Codes oder Werte sollen sich gegenseitig ausschliessen,
jedenfalls auf derselben Achse (Prinzip der Disjunktivität).
Die Forderung der Disjunktivität zwingt dazu, klare Begriffe zu
verwenden, führt aber (vorerst) zu zwei Nachteilen:
- die Zahl der
beschreibbaren Zustände entspricht genau der Zahl der Begriffe (oder
Codes). Mehr Zustände bekommen wir - mit einer Achse - nicht. Wenn wir
eine Natur annähernd präzise beschreiben wollen, erhalten wir deshalb
bald eine inflationäre Anzahl von "Schubladen", mit denen wir schnell
nicht mehr in praktikabler Weise umgehen können.
- Wenn wir ein
hierarchisches System abbilden wollen, müssen wir uns darüber einigen,
was wir als oberstes Unterscheidungsmerkmal betrachten. Dieses
definiert dann die oberste Etage der Oberbegriffe und ein anderes
Merkmal kann auf dieser Etage nicht mehr Oberbegriffe bilden - und
auch auf tieferen Schichten nicht mehr, wenn sich die Merkmale
überschneiden, dh. wenn sie kombinierbar sind (siehe Beispiel weiter
unten). Dann entstehen entweder unnötige Wiederholungen oder die
Disjunktivität wird gebrochen.
Zur
Illustration des zweiten Nachteiles kann ein Blick auf das
Inhaltsverzeichnis des ICD-10 Codes dienlich sein: Kapitel I fasst
Infektionen zusammen, Kapitel II Neubildungen und Kapitel IV
Stoffwechselkrankheiten. Ganz allgemein kann man von grundsätzlichen
pathophysiologischen Gruppen sprechen, die sich mehr oder weniger
ausschliessen. Die Kapitel III, VI, VII, VIII usw. beziehen sich
hingegen auf einzelne Organe/Organsysteme (die sich ebenfalls wieder
gegenseitig ausschliessen), wie Augen, Ohren, Kreislaufsystem usw. Wir
haben also zwei Typen von sich gegenseitig ausschliessenden
Oberbegriffen [4] . Untereinander sind diese
Typen aber kombinierbar. Es gibt Infektionen der Ohren und
Neubildungen der Augen. Wo im hierarchischen Baum sollen sie gesucht
werden? Bei den Neubildungen oder bei den Augenkrankheiten? Diese
Unklarheit auf der obersten Ebene setzt sich auf den tieferen Ebenen
fort und ist eine der Ursachen der vielen Unklarheiten, die der
Anwender eines solchen pseudohierarchischen Codes immerwährend
antreffen wird. Die historisch in langer Tradition gewachsene ICD-10
ist sich dieser Unklarheiten zwar in vorbildlicher Weise bewusst und
versucht den Anwender mit vielen "Exklusiva", "Inklusiva" [5] und anderen Kommentaren zu
führen, und - gewissermassen als "Clou" - das hierarchische Modell
selber mit der "Kreuz-Stern" Klassifikation [6] zu überlisten. Ob das
Handling allerdings durch das komplizierte Regelwerk und die sehr
inkonsistent realisierte "Kreuz-Stern"-Idee
einfacher wird, darf bezweifelt werden.
Dem ersten Nachteil, dass mit einer Anzahl z von Begriffen nicht mehr als z unterschiedliche Zustände beschrieben werden können, und - mindestens in gewisser Weise - auch dem zweiten Nachteil, den wir als "Typenvermischungsproblematik" ansprechen könnten, hilft der zweite Typ Klassifikationsmodell ab, welcher die Eigenschaft der Multidimensionalität einführt:

|
Die Welt der
Begriffe wird in diesem einfachen Beispiel nach zwei Merkmalen
geordnet (A und B). Die zwei Merkmale spannen gleich zwei Dimensionen
eine Fläche auf und jeder Ort der Fläche (jedes Feld) ist mit jeder
der beiden Dimensionen in der Weise verbunden, dass jedem Ort ein
genau bestimmter Wert in jeder Dimension zukommt. Umgekehrt gibt es
für jede Dimensionswertekombination genau ein Feld. Dieses Arrangement
hat einige Vorteile gegenüber dem linearen Vormodell. Zur
Veranschaulichung stelle man sich vor, dass das Merkmal A sich auf
infektionserregende Keime, das Merkmal B auf Organe des Körpers
beziehe. Mögliche Werte für das erste Merkmal (Keime=A) wären dann:
- Staphylokokken, Tuberkulose-Bakterien, Pneumokokken, Grippeviren, HI-Viren, Meningokokken, Gonokokken, Malariaplasmodien
Für zweite
Merkmal (Organe=B) wären folgende Werte denkbar:
- Blut, Lunge,
Hirnhäute, Nasennebenhöhlen, Knochen, Haut, Nieren, Leber, usw.
Die Felder,
welche von diesen beiden Merkmalen beschrieben werden, kombinieren nun
je einen Wert A mit einem Wert B, zB:
-
Staphylokokken / Lunge
-> Staphylokokkenpneumonie
-
Tuberkulose / Knochen
-> Knochentuberkulose
Durch die
Multidimensionalität können somit zwei Merkmale A und B unabhängig [7]
voneinander unterschiedliche Werte
annehmen. Die beiden Merkmale [8] spannen eine
2-dimensionale Ebene auf. Die Zahl der Felder entspricht der Zahl der
Zustände der Realität, welche das Modell beschreiben kann. Wenn a die
Zahl der Werte von Merkmal A und b die Zahl der Werte von Merkmal B
ist, so kann das Modell mit a + b unterschiedlichen Werten oder Begriffen a *
b unterschiedliche
Zustände beschreiben. Mit anderen Worten: Von der Zahl der zur
Beschreibung notwendigen Begriffe zur Zahl der damit beschreibbaren
Begriffe findet eine Vermehrung statt, welcher dem Sprung von der
Addition zur Multiplikation entspricht. Mit den im genannten Beispiel
vorliegenden 16 Begriffen (8 von Merkmal A und 8 von Merkmal B) können
64 (8*8) realitätsbezogene Zustände (Felder, Merkmalskombinationen)
beschrieben werden. Mit mehr Achsen und mehr Werten pro Achse wird die
Vermehrung noch augenfälliger. Ein einachsiges Begriffsmodell müsste
(und muss, siehe ICD) jeden kombinierten Zustand einzeln aufzählen und
wird dadurch unhandlich und überladen.
Der Zahl der
Dimensionen [9] ist dabei im Prinzip keine
Grenze gesetzt. Ein dreidimensionales Modell kann mit a+b+c
unterschiedlichen Begriffen a*b*c unterschiedliche Zustände
beschrieben. Bei vier Merkmalen wird die Felderzahl noch höher. Je
mehr Dimensionen vorhanden sind, umso stärker wird der Gewinn an
Beschreibungsmöglichkeiten.
Eine der
wichtigsten Fragen beim mehrdimensionalen Modell ist, welche Merkmale
[10] als dimensionale Achsen
gewählt werden sollen. Die SNOMED [11] zB, ein sehr ausgefeiltes
multidimensionales Codewerk, ursprünglich der Pathologen, verfügt in
der Version 2 über sieben Achsen [12] :
- M-Code:
Morphologie: welche Gewebsveränderung ist feststellbar (Entzündung,
Neoplasie usw.)
- E-Code:
Aetiologie: welche Ursache (z.B. Keime wie oben)
- T-Code:
Topologie: welcher Ort (z.B. Lunge, wie oben)
- F-Code:
Funktion (z.B. Hyperventilation)
- D-Code:
Disease (Krankheit, z.B. Gürtelrose)
- P-Code:
Procedure (Massnahme, z.B. Resektion)
- J-Code: Job
(Beruf, z.B. Goldschmid)
Der
mehrdimensionale Code erkauft sich die Vielfalt seiner
Realitätsbeschreibung mit dem geringfügigen Nachteil, dass ein
bestimmter Zustand nicht mit einem Code sondern mit einer
Code-Kombination beschrieben wird. Bei der ICD reicht ein Code zur
Beschreibung einer Krankheit, bei der SNOMED sind es einer, zwei oder
mehr [13] .
Unterschied zwischen dem
hierarchischen und dem mehrdimensionalen System
Die Nennung von
3 Codes bzw Begriffen in der SNOMED bedeutet nicht das gleiche wie die
Nennung von Begriff und Oberbegriffen in einem hierarchischen System.
Beide Male werden mehrere Begriffe genannt. Im hierarchischen System
sind die zusätzlichen Begriffe Oberbegriffe, auf welche durch den
Unterbegriff implizit immer geschlossen werden kann, im Fall eines
SNOMED-Tripletts sind die drei Begriffe hingegen voneinander
unabhängig.
Ein
eindimensionales System kann auch mehrdimensional erscheinen, nämlich
eine Hierarchie zweidimensional. Diese Zweidimensionalität ist aber
nur vorgetäuscht, da in der zusätzlichen Dimension keine zusätzlichen
Information steckt (siehe oben). Beim echten mehrdimensionalen System
steckt aber in jeder Dimension unabhängige Information.
Zur Veranschaulichung: Bei einem echten zweidimensionales System können die Achsen als 1-dimensionale Subsysteme gesehen werden, welche ihre eigenen Hierarchien haben. Hier folgt ein Graph eines 2-dimensionalen Systems mit den zwei Merkmalen (Typen/Achsen/ Dimensionen/Freiheitsgraden) Organ und Keim:

|
3: mehrdimensionales,
multifokales, unipunktuelles Modell
Das
beschriebene einfache multidimensionale Modell hat (vorerst) zwei
Nachteile:
-
"irrelevante", d.h. nicht belegbare Felder können entstehen.
- wir haben Mühe, uns über die Zahl der Achsen zu einigen
Mit den Achsen
ist es nämlich wie weiter oben beschrieben mit den Begriffen (oder
Schubladen oder Feldern). Wenn wir zuviele erlauben, dann wird das
System unhandlich, wenn wir zuwenige haben, wird es unscharf.
Die "Unschärfe"
einer Achse bedeutet, dass sie nicht mehr wirklich "linear" ist. Das
heisst: Die Werte (Begriffe) auf den Achsen sind nicht mehr wirklich
vom selben Typ, was sich darin äussert, dass die Hierarchien, die auf
dieser Achse Oberbegriffe bilden, nicht mehr eindeutig sind. Es
geschieht also genau das, was im Vorkapitel als negativ für das
unidimensionale Model beschrieben wurde. Als Lösung wurde dort
angeboten, den Typ zu entwirren und die Zahl der Achsen zu vermehren.
Wir müssen also beim Auftreten von Unschärfe die Achsenzahl vermehren.
Die Frage ist, ob die Zahl der Achsen nicht ins Unendliche vermehrt
werden muss, bzw. wie mit einer sehr grossen Zahl von Achsen handlich
umgegangen werden kann.

|
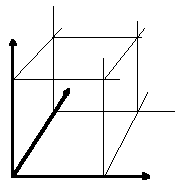 |
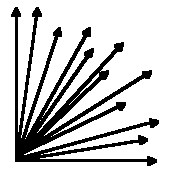 |
| 2-achsiges System | 3-achsiges System | 12-achsiges System [14] |
Begriffe können
im 2-achsigen System sowohl Abschnitte auf den beiden Achsen wie auch
Felder besetzen, im 3-achsigen System zusätzlich auch Würfel. Einen
12-dimensionalen Würfel können wir uns räumlich schlecht vorstellen,
ebensoschlecht 12-dimensionale Begriffe (die ja dann je zwölf
elfdimensionale Oberbegriffe hätten, und diese wieder je elf
zehndimensionale Ober-Oberbegriffe mit ..). Trotzdem treffen wir, wie
oben ausgeführt, unweigerlich auf solche hochdimensionalen "Ungetüme",
nicht nur theoretisch, sondern - wie sich im praktischen Umgehen mit
medizinischen Terminologien zeigt - auch ganz konkret. Die komplexe
Terminologie ist in der Medizin der Normalfall. Das beschriebene
Dimensions-Problem hat allerdings eine relativ einfache Lösung. Dabei
werden beide Nachteile, derjenigen der "irrelevanten" Felder wie
derjenige der Unhandlichkeit hochachsiger Darstellungen gleichzeitig
behoben.
Irrelevante
(oder nicht belegbare [15] ) Felder enstehen dort,
wo Kombinationen von Werten keinen Sinn ergeben. Hierzu ein Beispiel:
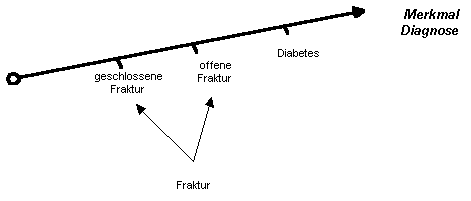
" Fraktur
" sei ein Wert auf der Achse " Diagnose ". Dieser Wert kann sich kombinieren mit einem Wert auf
einer anderen Achse, welche den Zustand der Hautbarriere bezeichnet
und zwei Werte kennt, nämlich " offen " und " geschlossen ". [16] " Diabetes mellitus " ist eine
andere Diagnose. Die Achse " offen/geschlossen " ist nun
schlecht mit " Diabetes
" kombinierbar, d.h. es hat keinen Sinn
von einem " offenen
" oder einem " geschlossenen Diabetes " zu
sprechen.
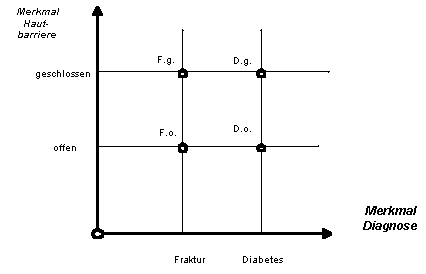 |
Die Punkte D.g. und D.o. (geschlossener und offener Diabetes) des obenstehenden Graphen sind im Gegensatz zu den Punkten F.g. und F.o. sinnlos. Die multiaxiale Begriffsrepräsentation lässt sie aber entstehen. Eine mögliche Lösung wäre:
 |
1.
Frakturen haben noch andere Merkmale ausser dem Zustand der
Hautbarriere. Z.B. spielt die Gelenkbeteiligung eine Rolle, die Zahl
der Knochenfragmente, der betroffene Knochen usw. Diese Merkmale sind
praktisch beliebig miteinander kombinierbar und lassen sich nicht in einer Hierarchie ordnen [17]
, sondern sind eben multidimensional.
2.
Das Merkmal "offen/geschlossen" spielt nicht nur für
Frakturen eine Rolle, sondern kommt auch andernorts vor - z.B. bei
offener und geschlossener Lungentuberkulose, kann also nicht in die
Hierarchie obligat unterhalb der
Fraktur eingeordnet werden.
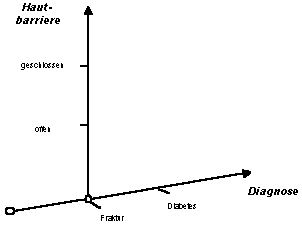
Deshalb muss die dargestellte "Einhierarchisierung" des Merkmals aufgegeben werden. Die Lösung liegt in der Beibehaltung der individuellen Achse, allerdings in einem Modell, in dem nicht alle Achsen zentral zusammentreffen, sondern in einem Modell, in dem die Achsen fokal bei bestimmten Werten angesetzt sind, wobei die gleiche Achse an mehreren Orten angesetzt werden kann:
|
Die Achse der Diagnosen (mit den Werten "Fraktur" und "Diabetes") ist am Wert "Fraktur" mit der Achse "offen/geschlossen" (="Hautbarriere") verknüpft. Der Wert "Fraktur" ist gewissermassen der Fokus für diese und weitere Achsen. Diese Art Darstellung erlaubt im Gegensatz zum einfachen multidimensionalen Modell nicht nur einen zentralen Fokus, sondern mehrere Foci zur Verknüpfung der Achsen [18] .
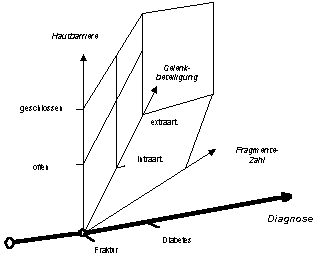
|
Dadurch, dass
die Achsen vom Zentrum in die Peripherie geschoben werden, ist der
Nachteil der Unhandlichkeit der Vielachsigkeit behoben. Jede Achse ist
genau dort wo sie sein muss.
Der zweite
Nachteil, das Entstehen von irrelevanten Feldern ("offener Diabetes")
wird dadurch vermieden, dass nicht mehr die Kombinationen von allen
Achsen gelten, sondern nur noch Kombinationen, für welche die
Merkmalsachsen explizit vorgesehen sind. So wie die Forderung nach Disjunktivität
durch die Multiaxialität erreicht werden kann, kann die
Forderung nach vollständiger Besetzbarkeit durch die Multifokalität
der Achsen erreicht werden.
Disjunktivität
und vollständige Besetzbarkeit sind gegenläufige Forderungen und erst
ihre gemeinsame Einlösung erlaubt ein plastisches Ordnen der Begriffe.
Die Begriffe und ihre Relationen werden in einem Modell dargestellt
und erlauben ein plastisches, realitätsnahes Modellieren der
darzustellenden Materie.
Vorkommen
des multiaxialen [19]
, multifokalen Modells:
Systeme der
beschriebenen 3. Generation sind sehr verbreitet, allerdings weniger
bei medizinischen Klassifikationen, als vielmehr bei:
- relationalen
Datenbanken
-
Objektorientierter Programmierung
-
Frame-Systemen
J.F.SOWA [20]
zeigt die Verwandtschaft der inneren
Strukturen dieser drei Konzeptdarstellungsmöglichkeiten. Natürlich
sind RDB, OOP [21] und Frames [22] drei sehr
unterschiedliche Welten mit unterschiedlichen Absichten, Stärken und
Möglichkeiten. Trotzdem sind sie verwandt, was die Strukturierung
ihrer Datenkonzepte anbelangt, die aufeinander abbildbar sind. Die
Datenkonzepte sind die Infostatik, d.h. das
"Schubladensystem", also das Klassifikationsmodell, wie es uns hier
interessiert. Was die OOP bezüglich Methodenhandling von den anderen
unterscheidet, hat nichts mit dieser Infostatik zu tun, sondern ist
bereits Infodynamik, d.h. zeitlicher
Umgang mit den Daten, d.h. das Mitteilen, Bearbeiten und Verändern von
Daten. Wie die Daten im Moment jedoch angeordnet [23] sind, das ist Infostatik,
und in dieser Datenanordnung unterscheiden sich RDB, KL-1 und OOP
nicht. Sie unterscheiden sich aber alle zusammen gleichermassen vom
simplen monohierarchischen und vom mehrdimensionalen, jedoch
unifokalen Modell. RDB, KL-1 und OOP sind Beispiele für die dritte
Generation von Datenanordnung, sind multiaxiale, multifokale Systeme.
In Anbetracht
der Ausdehnung und Komplexität der medizinischen Terminologie und auch
in Anbetracht der Bedeutung der Medizin für unser Leben, ist es
erstaunlich, dass gerade auf diesem Gebiet bisher kaum Anstrengungen
unternommen worden sind, die Klassifikationen und Terminologien
realitätsnaher anzupacken als dies etwa durch die ICD-9 oder die
ICD-10 möglich ist. Man würde denken, gerade in der Medizin gäbe es
ein Bedürfnis dafür. Neben vielen anderen, hier nicht näher
auszuführenden Gründen für die Unterlassung, gibt es einen verborgenen
Hauptgrund: Wer oberflächlich hinsieht, gibt sich mit
monohierarchischen Systemen zufrieden. Wer aber genau hinsieht, der
kapituliert und wendet sich "praktischeren" Fragen zu. Denn auch die
Klassifikationen der 3. Generation sind für die Medizin noch
unzureichend. Mit anderen Worten:
Medizinische Probleme können
auch mit Modellen der 3. Generation nicht klassifiziert werden.
Die Gründe dafür und den
Lösungsansatz zeigt das nächste Kapitel.
4: multifokales, multipunktuelles Modell
Wir haben gesehen, wie die Forderung
nach Disjunktivität den Sprung vom monohierarchischen zum
multidimensionalen Modell nahelegte. Die Forderung nach
vollständiger Besetzbarkeit andererseits hat dann die Rolle der
Dimensionen wieder eingeschränkt und den Achsen einen gekapselten
(fokalen) Geltungsbereich zugewiesen. Wenn wir mit solchen Systemen
arbeiten, sehen wir, dass wir erneut Probleme bekommen, und diese
stehen wieder mit der Forderung nach Disjunktivität im Zusammenhang,
nur dass es jetzt nicht mehr reicht, eine neue Achse zu bauen. Hierzu
ein Beispiel:
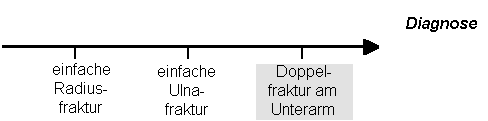
Knochenfrakturen treten an
bestimmten Knochen auf. So gibt es am Unterarm Frakturen der Elle
(Ulna) und der Speiche (Radius). Im weiteren besteht die Möglichkeit,
dass beim gleichen einen Unfall beide Knochen brechen. Es gibt dann
eine Hospitalisation, eine Operation, eine Rechnung und auch eine
Diagnose: Doppelfraktur des Unterarms.
|
Die Doppelfraktur des Unterarms
ist natürlich etwas anderes als die Summe einer Radius- und einer
Ulnafraktur. Der Patient braucht nicht zwei, sondern nur eine
Hospitalisation, wird nur einmal operiert, braucht nur eine Narkose.
Von den finanziellen und medizinischen Konsequenzen her ist das alles
andere als eine sophistische Haarspalterei. Und es ist ganz klar: Das
Ganze ist nicht das gleiche wie die Summe der Teile. Deshalb nehmen
wir die "Doppelfraktur UA" als einen eigenen Wert des Merkmals/der
Achse "Diagnose" auf.
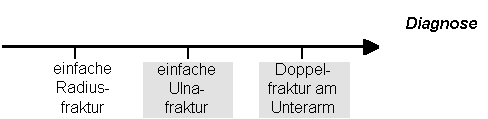
Doch diese Einteilung befriedigt nicht. Zwar können wir jetzt klar die Doppelfrakturen von den einfachen Ulnafrakturen trennen. Das Prinzip der Disjunktivität scheint erfüllt und wir können alle Frakturen klar zuordnen. Wenn wir jedoch nach der erfolgreich durchgeführten Zuordnung alle Ulnafrakturen in unserem Krankengut finden wollen, müssen wir die Doppelfrakturen - quasi als ein Spezialfall der Ulnafrakturen - ebenfalls mit einbeziehen.
|
Das
Diskjunktheitsproblem schlüpft damit - wenn auch nur bei der
Auswertung - durch die Hintertür wieder herein. Doch das ist nicht
alles. Die Doppelfrakturen sind ja nicht nur ein Spezialfall der
Ulna-, sondern auch ein Spezialfall der Radius-frakturen. Wirklich
korrekt (vorerst) wäre also nur die folgende Mengendarstellung:

|
Hier
überschneiden sich die Menge der Ulna- und der Radiusfrakturen und die
Unterarmdoppelfrakturen bilden ihre Schnittmenge. So verhält es sich
in Wirklichkeit. Die Forderung nach Diskjunktivität ist damit
allerdings unerfüllt. Wir könnten zwar - wenn wir die obige
Mengendarstellung im Kopf haben, oder im Computersystem, und zwar
explizit - auf der Achse "Diagnose" drei Orte (Codes) für die drei
Arten von Diagnosen vergeben und damit die Realität relativ korrekt
einfangen. Nur:
- Das Prinzip
der Disjunktivität, welches für ein Merkmal voraussetzt, dass die auf
seiner Merkmalsachse den Merkmalsausprägungen zugeordneten Objekte
voneinander unabhängige Mengen bilden, dieses Postulat bleibt grob
verletzt. Und die Forderung nach Disjunktivität ist nicht einfach
irgendein theoretisches Postulat. Erst wenn eine eindeutige Zuordnung
in der Praxis möglich ist, ist eine Klassifikation sinnvoll.
- Die
mengenmässigen Zusammenhänge müssten bei dieser Darstellung irgendwo
explizit festgelegt werden. Jeder, der die Klassifikation im
Einzelfall durchführt, muss die Regeln kennen, sonst klassiert er
falsch. Er darf also zB. nicht eine einfache Ulnafraktur klassieren,
wenn zusätzlich der Radius gebrochen ist, und umgekehrt. In beiden
Fällen muss er die Ulna- bzw Radiusfraktur bei der Doppelfraktur
einordnen. Zusätzlich muss aber auch der Auswerter die Regeln kennen.
Wenn er die Radiusfrakturen sucht, muss er die Unterarmdoppelfrakturen
in die Suche miteinbeziehen und sich dabei überlegen, was er
möglicherweise jetzt noch vergessen hat.
-
Mehrfachverletzungen sind keineswegs seltene, statistisch
vernachlässigbare Ausnahmen, sondern sie sind im Gegenteil sehr
häufig. Viele davon haben eigene Namen (zB. Monteggiafraktur, unhappy
triad, Weber-Fraktur). Bei Knochenverletzungen werden oft Haut, Nerven
und Sehnen mitverletzt. Im Bereich der Inneren Medizin ist es genau
gleich. Die Multimorbidität ist die Regel. Viele Diagnosen kommen
schon fast regelmässig kombiniert vor (z.B. Adipositas, Diabetes und
Hypertonie samt Folgen beim sog. Metabolischen Syndrom). Viele
Krankheiten kennt man überhaupt nur als Syndrome, also Kombinationen
von Symptomen.
- Weil
Multimorbidität und Mehrfachverletzungen die Regel sind, ist die
Klassifikation von Diagnosen so schwierig und sind Fehler, wenn der
einzelne Anwender codiert, praktisch unausweichlich. Der
Resourcenbedarf für diese Arbeit wird gewaltig unterschätzt.
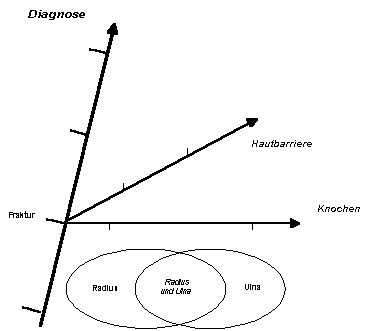
Die obige Abbildung ist in einer weiteren Hinsicht nicht ideal: Die Lokalisation ist nicht die einzige Eigenschaft einer Fraktur. Frakturen haben viele weitere Merkmale (wie die Intaktheit der Hautbarriere, usw.), welche sich mit der Lokalisation praktisch beliebig kombinieren. Wie bereits bei der Vorstellung des multifokalen Typs erklärt, ist es sinnvoll, "Fraktur" als einen Fokus zu betrachten, in den sich die für diesen Fokus relevanten Achsen treffen, u.a. die Achse, welche den gebrochenen Knochen bezeichnet. Dies führt (vorerst) zu folgender Abbildung:
|
Etwas stört aber: Auf der Achse der Diagnosen konnten wir uns einen Wert für die Doppelfraktur vorstellen. Auf der Achse der Knochen ist ein Wert für Doppelknochen nicht mehr sinnvoll. M.a.W: Wir müssen das Prinzip der Disjunktivität brechen - allerdings kontrolliert und gezielt:
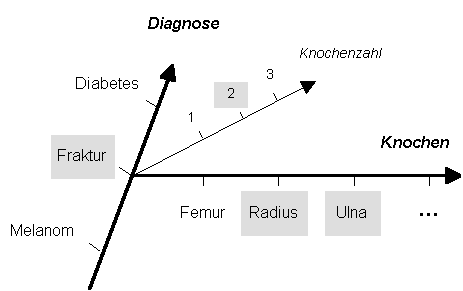
|
Im multipunktuellen Modell kann
also - im Gegensatz zu den drei bisher besprochenen Modellen - ein
Merkmal (eine Achse) gleichzeitig mehrere Ausprägungen (Werte)
aufweisen. Dabei müssen die Werte nicht benachbart sein, sich also
nicht unter einen gleichen Oberbegriff dieser Achse subsummieren
lassen. Mengen (Sets) beliebiger Werte auf der gleichen Achse können
zusammengestellt werden und bilden - als Menge - die Ausprägung dieses
Merkmales für eine inhaltliche Entität (Klasse).
Dieser Bruch der Disjunktivität
und Eindeutigkeit innerhalb des Merkmals muss jedoch im Begriffssystem
vermerkt werden. Im gezeigten Beispiel wird deshalb die
Mehrfachnennung auf der Achse "Knochen" durch den Wert "2" auf der
Achse "Knochenzahl" angezeigt. Dem System müssen die häufigsten
Mehrfachdiagnosen bekannt und als "Alias" verfügbar sein. Es muss -
insbesondere den auswertenden Statistikern - klar sein, dass auf
verschiedenen Ebenen "gesprochen" wird. Diese Klarheit kann durch
verschiedene Lösungen verschieden perfekt erreicht werden, genauso wie
das vorher besprochene multifokale Modell verschiedene Ausformungen
(KL-1, OOP-Sprachen, RDB's, Partikelmodell der CSL [24] usw.) erfuhr. Ohne eine
gebührende Berücksichtigung der Multipunktualität kann jedoch kein
Klassifikationssystem bestehen.
Unterschied zwischen der
multiaxialen und der multipunktuellen Lösung
Weshalb muss die
Multipunktualität eingeführt werden? Die Forderung nach Disjunktivität
hat doch bereits einmal zu einem neuen Modell geführt. Weshalb kann
man die dortige Lösung - nämlich die Bildung neuer Achsen - nicht
erneut für das vorliegende Problem verwenden?
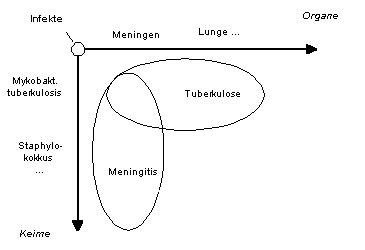
Zur Beantwortung der Frage hilft es, sich die Mengenverhältnisse und die Abbildung der Mengen in das dimensionale Gerüst vorstellen. Zuerst am Beispiel, das zur Einführung der Mehrdimensionalität geführt hat:
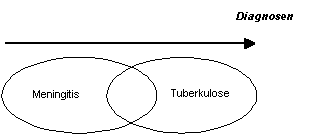 |
Meningitis und Tuberkulose sind beides einwandfreie medizinische Diagnosen. Sie überschneiden sich allerdings, d.h. sie sind nicht disjunkt. Die Schnittmenge ist die tuberkulöse Meningitis.
|
Wenn man nun wie aufgeführt
die Mengen auf zwei Achsen verteilt, bekommt man eine weitgehende
Aequivalenz der Mengen- zu den Achsenverhältnissen. M.a.W: Man kann
die real existierenden Mengenbeziehungen einwandfrei auf ein
Koordinatensystem abbilden, sobald man eine zusätzliche Achse
einführt.
Bei den Unterarmfrakturen sind die Verhältnisse grundlegend anders:
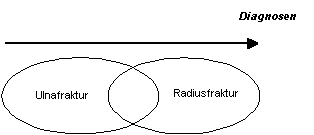 |
Auf den ersten Blick besteht zwar eine weitgehende Aehnlichkeit zu den
vorigen Verhältnissen: Ulnafraktur und Radiusfraktur sind einwandfreie
medizinische Diagnosen. Sie gehören beide zu einer gleichen Klasse
(den Frakturen). Sie sind nicht ganz disjunkt, und ihre Schnittmenge
sind die UA-Doppelfrakturen. Aber hier hört die Analogie auf, und es
erweist sich, dass hier die Disjunktivität von einem grundlegend
anderen Charakter ist als am Vorbeispiel. Die Disjunktivität
lässt sich nämlich mit einer Vermehrung der Achsen NICHT sinnvoll zum
Verschwinden bringen.
Hier mein gescheiterter Versuch die Mengenbezüge analog zum vorhergehenden Beispiel auf ein zweiachsiges Koordinatensystem abzubilden:
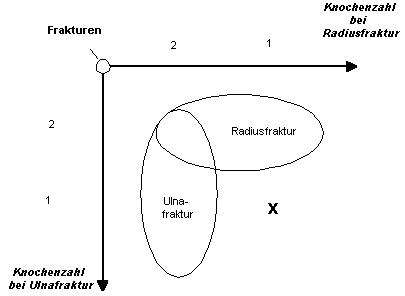 |
Die horizontale Achse muss den Unterschied der Schnittmenge
(=UA-Doppelfraktur) zu den übrigen Radiusfrakturen thematisieren,
analog wie im Vorbeispiel der Unterschied der Schnittmenge
(=tuberkulöse Mengigitis) zu den übrigen Tuberkulosen thematisiert
wurde. Der erste Unterschied betraf das Merkmal "Organ". Jetzt liegt
der Unterschied in der Zahl der gebrochenen Knochen. Analog betrifft
der Unterschied in vertikaler Richtung die Zahl gebrochener Knochen
bei Ulnafraktur.
Diese Achsenbenennung macht aber
insgesamt keinen Sinn, was zB daran ersichtlich ist, dass der Ort, den
ich mit dem Kreuz gekennzeichnet habe, logisch paradox ist. Er würde
eine Fraktur bezeichnen, bei der ein Knochen gebrochen ist, und die
gleichzeitig eine Radius- und eine Ulnafraktur ist. Im Vorbeispiel der
Meningitis ist der entsprechende Ort aber nicht nur völlig frei von
jedem logischen Widerspruch, sondern er bezeichnet - ohne dass dies
speziell erwähnt wurde -eine Diagnose, die auch tatsächlich vorkommt,
nämlich die Staphylokokkenpneumonie.
Die logischen Widersprüche gehen
weiter: im Quadrant oben rechts findet sich eine einfache
Radiusfraktur. Das wäre aber nach dem Achsensystem eine Fraktur sowohl
mit einem Knochen (als Radiusfraktur) als auch mit zwei gebrochenen
Knochen (als Ulnafraktur!). Und wo zeichnete man eine Oberarmfraktur
ein? Die Verhältnisse im Vorbeispiel führen niemals in eine solche
Widersinnigkeit. Zwar gibt es Kombinationsmöglichkeiten, die nicht
wirklich vorkommen (zB Grippeviren in der Haut), aber ganz unmöglich
sind sie nicht und sie führen hauptsächlich nicht zu logischen
Widersprüchen im Koordinatensystem wie das Beispiel mit der
Unterarmfraktur.
Man mag einwenden, dass ich die
Achsen schlecht gewählt habe, doch der geneigte Leser möge selber
versuchen, geschicktere Achsen zu wählen, die zu keinem Widerspruch
führen. Die beobachteten Verhältnisse lassen mich annehmen, dass es in
der Natur der Disjunktivität einen prinzipiellen Unterschied gibt und
dass die Forderung nach Disjunktivität in den einen Fällen mit der
Einführung einer neuen Achse, in den anderen jedoch nur mit dem
prinzipiellen Akzeptieren der hier vorgestellten Multipunktualität
gelöst werden kann.
Die Rolle
von Klassifikationsmodellen (Reprise)
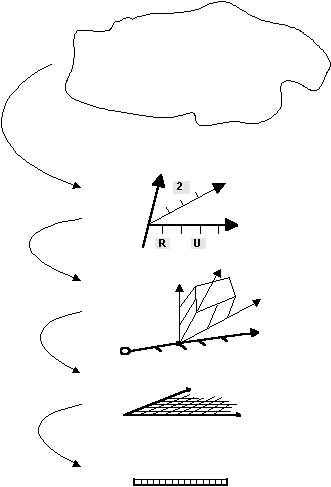
Weshalb klassieren wir? Wenn wir in der Realität eine grosse Zahl unterschiedlicher Objekte ansehen, müssen wir sie gruppieren, um ähnliche Fälle gleich behandeln zu können. Dabei soll die Komplexität der Realität möglichst präzise und einfach abgebildet werden. Die Modelle der 4. Generation kommen der Realität am nächsten:
|
Doch einfachere Modelle haben ebenfalls ihre Vorteile. Sie sind -
wenn keine Präzision verlangt wird - vor allem einleuchtender und
einfacher im Handling. Immer wenn wir handeln müssen, wollen wir
eine einfache Sicht, damit wir nicht durch die Komplexität verwirrt
werden. Auch sind nicht alle Aspekte gleich wichtig. Deshalb wollen
wir nur den wichtigsten Aspekt für die Einteilung der Dinge
verwenden und stützen uns in unseren Handlungen sinnvollerweise
nicht auf unwesentliche Details:
|
Simple Klassifikationen besitzen ohne Zweifel eine grosse
Attraktivität. Das Grundproblem zeigt aber folgendes Bild:
|
Eine einfache, sogar eine
unidimensionale Klassifikation kann trotzdem sinnvoll sein - aber nur
im Hinblick auf eine jeweilige Arbeit, auf ein jeweiliges Ziel. Eine
andere Fragestellung ergibt eine andere Sicht und somit eine andere
unidimensionale Klassifikation.
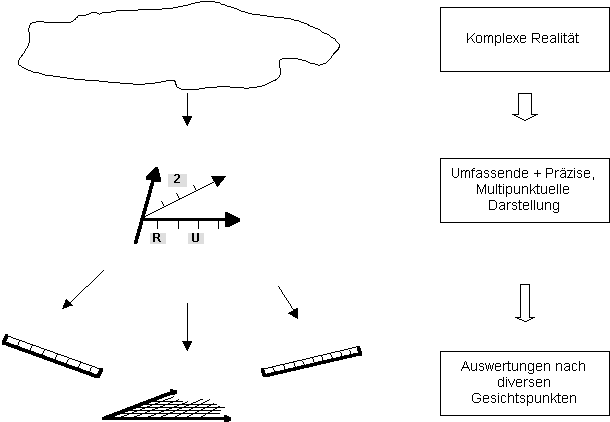
Beide Forderungen - diejenige nach grösster Nähe zur Komplexität und grösster Präzision in der Abbildung der Realität einerseits und diejenige nach grösster Einfachheit der Darstellung andererseits - können gleichzeitig berücksichtigt werden, wenn Klassifikationen unterschiedlicher Natur gemischt werden. Dabei müssen die unterschiedlichen Systeme aber unbedingt am richtigen Ort eingesetzt werden:
|
Primär wird natürlich in das realitätsnaheste Modell abgebildet. Je
nach dem Zweck der Untersuchung werden die gewonnenen Informationen
dann aber in einfachen multi- oder unihierarchischen Einteilungen
angeboten. Wenn die Information primär klar in ein widerspruchsfreies
multifokales, multipunktuelles Klassifikationssystem eingegeben wird,
ist eine spätere Abbildung in beliebige Systeme tieferer Stufe einfach
möglich, da immer klare Regeln für diese Abbildung gefunden werden
können [25] . Wenn primär in ein
komplexes Klassifikationssystem eingeteilt wird, ist man bei der
späteren Interpretation nicht eingeengt, da eine flexible Anordnung
der Information, genau nach den Gesichtspunkten, welche die aktuelle
Aufgabe erfordert, auf jeden Fall möglich ist.
Rekapitulierend sehen wir bei
der Anordnung der Begriffe in Klassifikationen eine Entwicklung mit
zunehmender Komplexität und Realitätsnähe. Die Systeme der ersten
Generation, die hierarchischen Systeme, enthalten je einen
Freiheitsgrad. Die mehrdimensionalen Systeme der zweiten Generation
enthalten n Freiheitsgrade, für jede Dimension einen. Bei der
dritten Generation sind die Freiheitsgrade nicht mehr unabhängig
voneinander, sondern bilden ein Netz. Je nach Ausfall des einen
Freiheitsgrades (Wert auf der einen Achse) sind andere Freiheitsgrade
(Achsen) offen. Die Achsen berühren sich somit in mehreren Punkten
(Foci), weshalb wir die Systeme der dritten Generation multifokal
nennen. Bei der vierten Generation ist das Gewebe der Achsen (der
semantische Raum) von der gleichen Struktur wie bei der dritten
Generation. Auf einer Achse können bei der vierten Generation aber
mehrere Punkte gleichzeitig aktiv sein, d.h. mehrere Werte des
gleichen Typs gleichzeitig ausgewählt werden. Auf diese Weise können
zusammengesetzte Objekte wie z.B. Mehrfachdiagnosen logisch
widerspruchsfrei und computergängig dargestellt werden.
Anhang
|
Modellgeneration |
Dimensionalität/Axialität |
Fokalität |
Punktualität |
|
1.Generation |
eindimensional=uniaxial=Hierarchie |
- |
unipunktuell |
|
2.Generation |
mehrdimensional=multiaxial |
unifokal |
unipunktuell |
|
3.Generation |
mehrdimensional=
multiaxial |
multifokal |
unipunktuell |
|
4.Generation |
mehrdimensional=
multiaxial |
multifokal |
multipunktuell |
|
Modellgeneration |
Anzahl semantische Achsen |
Anzahl Achsenschnitt-punkte (=Foci) |
Anzahl Punkte |
|
1.Generation |
1 |
0 |
1 |
|
2.Generation |
n |
1 |
1 |
|
3.Generation |
n |
z |
1 |
|
4.Generation |
n |
z |
m |
[2] Man könnte annehmen, Codes hätten vor allem den Vorteil der Uebersichtlichkeit. Die Uebersichtlichkeit ergibt sich aber durch den Aufbau des Schubladensystems, nicht durch die Beschriftung der Schubladen.
[3] Natürlich ist "A" ein Buchstabe und keine Zahl. Rein informationstheoretisch unterscheidet er sich aber von einer Zahl lediglich darin, dass er aus 26 und nicht aus 10 Zuständen auswählt. Die lineare, diskrete, eindimensionale Anordnung bleibt bei diesem System erhalten.
[4] Wenn man alle Kapitel ansieht, sind es natürlich mehr als 2 Typen. Dies widerspricht der Aussage des vorliegenden Abschnittes jedoch wohl kaum.
[5] d.h. extensionalen Aufzählungen, siehe J.Ingenerf (1993): Benutzeranpassbare semantische Sprachanalyse und Begriffsrepräsentation für die medizinische Dokumentation. Infix, St.Augustin.
[6] ICD-10, Band II, S.22 (Urban-Schwarzenberg 1995)
[7] WINGERT bezeichnet unabhängige Mermale als orthogonal: F. WINGERT (1984): SNOMED Manual. Springer, Berlin.
[8] oder Achsen oder Dimensionen oder Freiheitsgrade, die vier Begriffe sind für die gesamte vorliegende Betrachtung weitgehend äquivalent
[9] oder Merkmale oder Achsen, siehe vorhergehende Fussnote
[10] oder Dimensionen oder Achsen, siehe vorhergehende Fussnoten
[11] ein typischer mehrdimensionaler Code. SNOMED = Standardized NOmenclature of MEDicine
[12] In der aktuellen Version 3 sind es 12 Achsen. Zur Achseninflation siehe das Folgekapitel.
[13] d.h dass zur Beschreibung einer Diagnose nicht in jeder Achse eine Ausprägung nötig ist.
[14] Die Hilfslinien, welche die einzelnen 12-dimensionalen "Würfel" umreissen würden, sind im 12-achsigen System im Gegensatz zum 3-achsigen (wegen kleineren praktischen Problemen) nicht mehr eingezeichnet.
[15] gemäss WINGERT. Siehe F.Wingert(1984): SNOMED Manual. Springer, Berlin.
[16] Bei einer offenen Fraktur ist die Hautbarriere verletzt und Fremdkörper und Keime können eindringen und Enztündungen verursachen. Offene Frakturen heilen deshalb schlechter und das Merkmal "offen/geschlossen" ist für Frakturen wichtig.
[17] Die ICD-10 simuliert für das Merkmal "offen/geschlossen" die Multidimensionalität mit einer fakultativen 5. Stelle, kann wegen ihrer prinzipiell hierarchischen Struktur aber nicht systematisch alle benötigten Merkmale analog, d.h. mit einer jeweils eigenen, zusätzlichen Stelle berücksichtigen.
[18] Die Foci sind in der Abbildung als kleine Kreise dargestellt. Der etwas grössere Kreis ganz links ist der zentrale Fokus - oder das Zentrum - des multifokalen Systems.
[19] Hier synonym mit mehrdimensional.
[20] J.F.SOWA (2000): Knowledge representation. logical, philosophical and computational Foundations. Brooks/Cole, Pacific Grove.
[21] RDB=relationale DatenBank. OOP= ObjektOrientierte Programmierung.
[22] M. Minsky.
[23] Inkl. der Vererbung, die ebenfalls zum 3.Generations-Modell und zur Infostatik gehört, hier aber aus Platzgründen nicht behandelt wird.
[24]
H. R. STRAUB (1994 ): Wissensbasierte
Interpretation, Kontrolle und Auswertung elektronischer
Patientendossiers. Kongressband der IX. Jahrestagung der
SGMI, Nottwil.
[25] Umgekehrt geht das natürlich nicht